Embark on a captivating journey into the realm of quantum mechanics with Introduction to Quantum Mechanics Griffiths 3rd Edition Solutions. This comprehensive guide unravels the complexities of quantum theory, providing a solid foundation for students and researchers alike.
Delving into the fundamental principles and applications of quantum mechanics, this resource empowers readers to navigate the intricacies of wave functions, operators, and quantum states. With a focus on clarity and depth, it illuminates the enigmatic world of atomic and molecular physics, spectroscopy, and chemical bonding.
1. Introduction to Quantum Mechanics

Quantum mechanics is a branch of physics that studies the behavior of matter and energy at the atomic and subatomic level. It emerged in the early 20th century, driven by the need to explain phenomena that could not be accounted for by classical physics.
The fundamental principles of quantum mechanics include the wave-particle duality of matter, the uncertainty principle, and the superposition principle. These principles challenge our classical understanding of the world and have led to the development of new technologies, such as lasers and transistors.
1.1 Historical Development
The roots of quantum mechanics can be traced back to the late 19th century, with the work of Max Planck on blackbody radiation. Planck’s hypothesis that energy is quantized in discrete units, called quanta, was a radical departure from classical physics.
This hypothesis laid the foundation for the development of quantum theory.
In the early 20th century, Niels Bohr proposed a model of the atom that incorporated the idea of quantized energy levels. This model successfully explained the spectrum of light emitted by hydrogen atoms and marked a significant advance in the understanding of atomic structure.
The development of quantum mechanics was furthered by the work of Erwin Schrödinger, Werner Heisenberg, and Paul Dirac. Schrödinger developed a wave equation that describes the behavior of quantum particles, while Heisenberg formulated the uncertainty principle. Dirac developed a relativistic theory of quantum mechanics that incorporated the principles of special relativity.
1.2 Fundamental Principles and Concepts
- Wave-particle duality:Matter exhibits both wave-like and particle-like properties. For example, light can behave as a wave or as a stream of particles called photons.
- Uncertainty principle:There are fundamental limits to the precision with which certain pairs of physical properties, such as position and momentum, can be known simultaneously.
- Superposition principle:A quantum system can exist in a superposition of multiple states simultaneously. For example, an electron can be in a superposition of being in two different locations at the same time.
2. Mathematical Formalism

The mathematical formalism of quantum mechanics provides a framework for describing and predicting the behavior of quantum systems.
2.1 Wave Function
The wave function is a mathematical function that describes the state of a quantum system. It contains all the information about the system, including its energy, momentum, and position.
The wave function satisfies the Schrödinger equation, a partial differential equation that governs the time evolution of the system.
2.2 Solving Schrödinger’s Equation
Solving Schrödinger’s equation for simple systems, such as the hydrogen atom, can provide insights into the behavior of quantum systems.
For example, solving the Schrödinger equation for the hydrogen atom yields the energy levels of the atom and the wave functions of the electrons in each energy level.
2.3 Operators
Operators are mathematical objects that represent physical quantities, such as energy, momentum, and position. They operate on wave functions to yield other wave functions.
Operators play a crucial role in quantum mechanics, as they allow us to calculate the values of physical quantities for quantum systems.
3. Quantum States and Observables
Quantum states are mathematical representations of the possible states of a quantum system. They are typically represented by wave functions.
Observables are physical quantities that can be measured for a quantum system. They are represented by operators.
3.1 Measurement, Introduction to quantum mechanics griffiths 3rd edition solutions
When an observable is measured, the quantum system collapses into one of its possible states. The probability of obtaining a particular outcome is given by the Born rule.
3.2 Uncertainty Principle
The uncertainty principle states that there are fundamental limits to the precision with which certain pairs of physical properties, such as position and momentum, can be known simultaneously.
The uncertainty principle has important implications for the interpretation of quantum mechanics.
4. Applications in Atomic and Molecular Physics
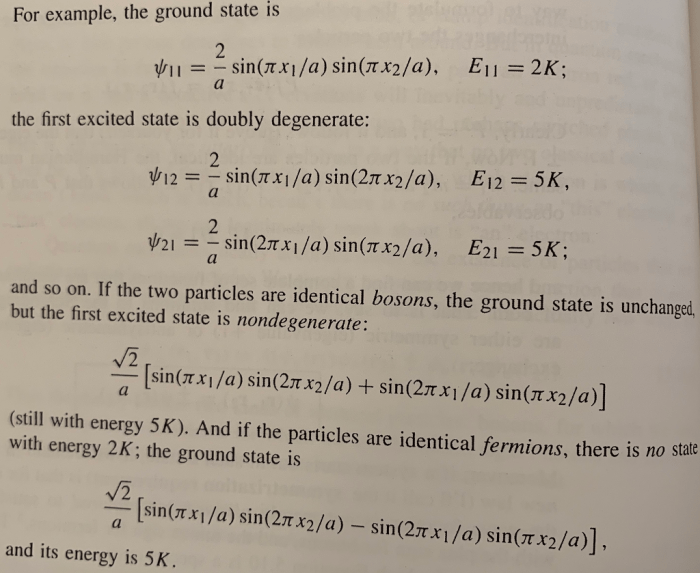
Quantum mechanics has a wide range of applications in atomic and molecular physics.
4.1 Atomic Structure
Quantum mechanics can be used to explain the structure of atoms, including the arrangement of electrons in energy levels.
The quantum mechanical model of the atom is based on the Schrödinger equation and the Pauli exclusion principle.
4.2 Molecular Bonding
Quantum mechanics can be used to explain the formation of chemical bonds between atoms.
The quantum mechanical model of chemical bonding is based on the valence bond theory and the molecular orbital theory.
4.3 Spectroscopy
Quantum mechanics can be used to explain the spectra of atoms and molecules.
Spectroscopy is a powerful tool for studying the structure and properties of atoms and molecules.
5. Extensions and Interpretations: Introduction To Quantum Mechanics Griffiths 3rd Edition Solutions

Quantum mechanics has been extended to include spin and relativity.
5.1 Spin
Spin is an intrinsic property of elementary particles. It is a vector quantity that has both magnitude and direction.
Spin can be explained by the Dirac equation, a relativistic wave equation that incorporates the principles of special relativity.
5.2 Relativity
Relativistic quantum mechanics is a theory that combines the principles of quantum mechanics and special relativity.
Relativistic quantum mechanics is necessary for describing the behavior of high-energy particles, such as those found in particle accelerators.
5.3 Interpretations
There are different interpretations of quantum mechanics, including the Copenhagen interpretation and the many-worlds interpretation.
The Copenhagen interpretation is the most widely accepted interpretation of quantum mechanics. It states that the wave function of a quantum system represents the state of knowledge about the system, rather than the state of the system itself.
The many-worlds interpretation is an alternative interpretation of quantum mechanics. It states that the wave function of a quantum system represents a superposition of all possible states of the system, and that each state exists in a separate universe.
FAQ
What is the significance of the wave function in quantum mechanics?
The wave function provides a mathematical description of the state of a quantum system, containing information about its position, momentum, and other properties.
How does the uncertainty principle impact quantum measurements?
The uncertainty principle states that certain pairs of physical properties, such as position and momentum, cannot be measured simultaneously with arbitrary precision.
What are the key applications of quantum mechanics in atomic and molecular physics?
Quantum mechanics plays a crucial role in understanding atomic and molecular structures, explaining phenomena such as electron configurations, chemical bonding, and spectroscopy.